
옵티마이저(Optimizer)
오차를 어떻게 줄여 나갈지 정하는 함수


경사하강법(Gradient Descent, GD)
- 가장 기본적인 Optimizer 알고리즘
- 학습률(learning rate)과 손실함수(loss function)의 순간기울기(gradient)를 이용하여 가중치(weight)를 업데이트하는 방법
- 학습률(learning rate)이 너무 크면 학습 시간이 짧아지나 전역 최솟값(Global minimum)에서 멀어짐
- 학습률(learning rate)이 너무 작으면 학습시간이 오래걸리고 지역 최솟값(Local minimum)에 수렴할 수 있음
- 한번 업데이트 할 때 마다 전체 데이터를 미분해야 하므로 계산량이 많음 (속도 느림)
- 학습률(learning rate)은 하이퍼 파라미터로, 하강하는 보폭(step)을 의미함
※지역 최솟값(local minimum) - 전역 최솟값(Global minimum)이 아닌 지역 최솟값(local minimum)으로 경사하강법이 끝나는 현상
배치 경사 하강법(Batch Gradient Descent, BGD)
- 전체 학습 데이터를 하나의 배치로 묶어 학습시키는 경사 하강법
- 전체 데이터를 통해 학습시키기 때문에, 가장 업데이트 횟수가 적음
- 전체 데이터를 모두 한번에 처리하기 때문에, 메모리가 가장 많이 필요함
- 전체 데이터에 대해 경사를 구하기 때문에 수렴이 안정적임
- 전역 최솟값(Global minimum)을 찾을 수 있는 장점이 있음


에포크 (Epoch)
- 인공 신경망에서 전체 데이터에 대해서 순전파와 역전파가 끝난 상태
- 문제지 모든 문제를 풀고, 채점하여 공부를 한번 끝낸 상태 (1Epoch)
- 에포크가 10이면 전체 데이터 단위로는 총 10번 학습한것 (문제지 10번푼셈)
- 에포크 횟수가 지나치게 많음 (과적합-Overfitting)
- 에포크 횟수가 너무 적음 (과소 적합-Underfitting)
배치 크기(Batch size)
- 배치 크기는 몇 개의 데이터 단위로 매개변수를 업데이트 하는지 의미
- 문제지에서 몇 개씩 문제를 풀고나서 정답지를 확인하는지 의미(문제를 풀고 정답을 보는 순간 부족했던 점 깨달으며 업데이트)
- 실제값과 예측값으로부터 오차를 계산하고 옵티마이저가 매개변수를 업데이트
- 업데이트가 시작되는 시점이 정답지/실제값을 확인하는 시점
- 문제가 1000개 있는 문제지의 문제를 100개 단위로 풀고 채점하면 배치 크기는 100
- 배치 크기가 100이면 100개의 샘플 단위로 가중치를 업데이트
- 배치 크기와 배치의 수는 다른 개념
- 전체 데이터: 1000, 배치 크기: 10, 배치수: 100 (1000/10=100)
※위에서 말한 배치의 수가 바로 이터레이션(Iteration)
※Batch size를 높게 줬을때, 컴퓨터가 제대로 학습하지 못한다면 컴퓨터의 메모리문제 때문에 Batch size를 낮춰줘야함
※ 32, 64, 128, 256, 512 메모리 사이즈에 맞춰서 설정(일반적으로 32가 성능이 가장 좋음)
(GPU/RAM에서 일반적으로 작동하는 방식이 2의 제곱이기 때문에 2의 제곱이 아닌 다른 숫자를 설정하면 비효율적이며 성능 저하가 일어날 수 있고, 많은 데이터를 처리 할 때 비효율성은 성능에 큰 영향을 미침)
이터레이션(Iteration)
- 한번의 에포크를 끝내기 위해서필요한 배치의 수
- 한번의 에포크 내에서 이루어지는 매개변수의 업데이트 횟수
- 전체 데이터 : 1000, 배치 크기 : 10, 이터레이션 : 100 (1000/10 = 100)
- 한번의 에포크 당 매개변수 업데이트가 100번 진행

학습률(Learning Rate, Lr)
- 학습률은 아주 중요한 하이퍼 파라미터(Hyper parameter)
- 학습률(Learning rate, Lr) or 보폭(Step size)로 불리는 스칼라를 곱해 다음 지점을 결정
- 학습률(Learning rate)이 클경우 데이터가 무질서하게 이탈하며, 최저점에 수렴하지 못함
- 학습률(Learning rate)이 작은경우 학습시간이 매우 오래걸리며, 최저점에 도달하지 못함

확률적 경사 하강법(Stochastic Gradient Descent, SGD)
- 전체 데이터를 사용하는게 아니라, 랜덤하게 추출한 일부 데이터 사용(더 빨리 자주 업데이트, 성능 개선정도를 빠르게 확인 가능)
- 기존에 경사 하강법의 문제인 불필요하게 많은 계산량으로 인한 속도 저하, 최적화 값을 찾기 전에 최적화 과정 멈춤을 보완함
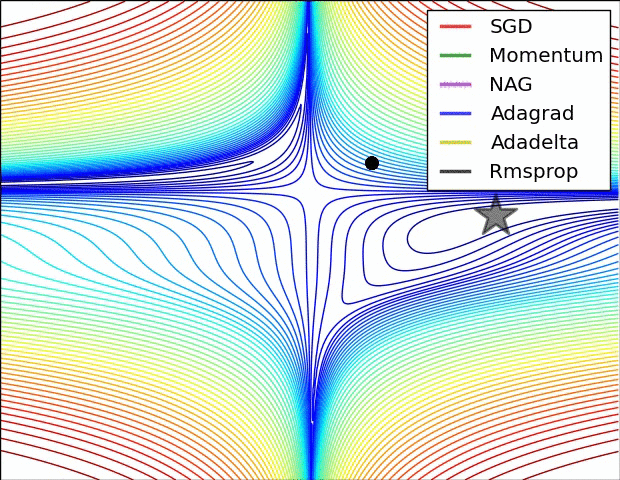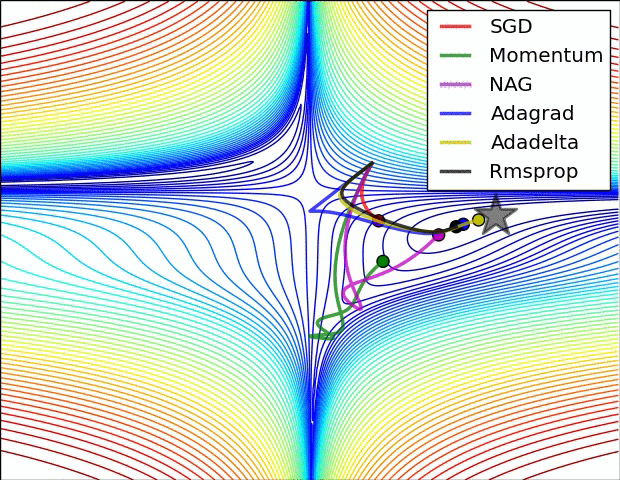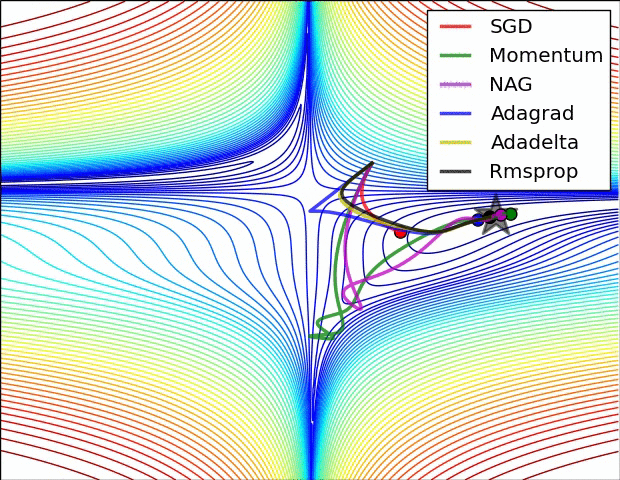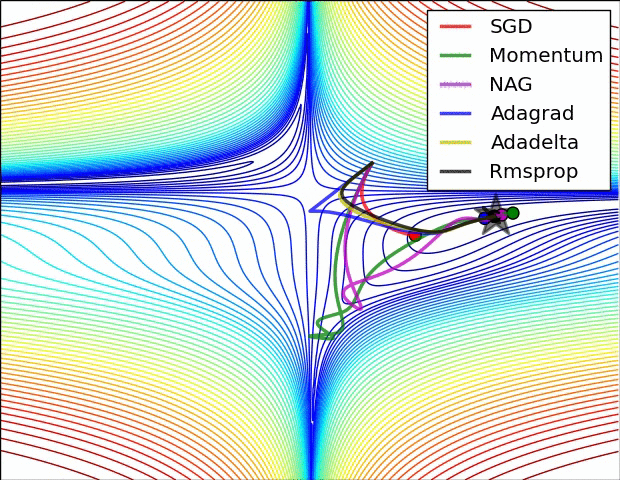
- 위 그림에서 경사 하강법과 SGD의 차이점을 보면 진폭이 크고 불안정해 보일 수 있지만 속도가 확연히 빠르고, 최적값에 근사한 값을 찾아냄
- 최소 cost에 수렴했는지의 판단이 상대적으로 어려움
- 지역 최솟값(local minimum)에 빠질 가능성을 줄일 수 있음

미니 배치 경사 하강법(Mini-Batch Gradient Descent)
- SGD와 BGD의 절충안으로, 전체 데이터를 batch_size개씩 나눠 배치로 학습
- BGD보다 계산량이 적어서 빠르며, SGD보다 안정적임 (Batch Size에 따라 계산량 조절 가능)
- Shooting이 적당히 발생함(Local Minima를 어느정도 피함)
※Shooting - 손실함수 값이 줄어들지 않고 오히려 커지는 현상
※손실함수 - 결과 값이 실제 값과 얼마나 차이가 있는지 계산하는 함수, 손실함수로 얻은 결과 값을 에러라고하는데, 손실함수의 값이 작을수록 학습이 잘된거라고 함
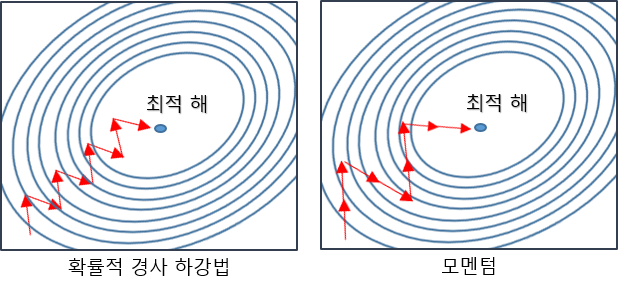
모멘텀(Momentum)
- 모멘텀(Momentum)이라는 단어는 '관성, 탄력, 가속도' 라는 뜻에서 유추할 수 있듯이 물리학의 법칙을 응용한 방법
- 오차를 수정하기 전 바로 앞 수정 값과 방향(+, -)을 참고하여 같은 방향으로 일정한 비율만 수정하는 방법
- 이전 이동 값을 고려하여 일정 비율만큼만 다음 값을 결정하므로 지그재그로 일어나는 현상이 줄고, 관성효과를 냄
- 지역 최솟값(local minimum)에 도달했을 때, 관성의 힘을 빌려 값이 조절되면서 지역 최솟값(local minimum)에서 탈출함

네스테로프 모멘텀(Nesterov Accelrated Gradient, NAG)
- 모멘텀이 이동시킬 방향을 정하면, 그 방향으로 미리 이동해서 기울기를 계산, 불필요한 계산량을 줄이고 정확도를 향상 시키는 방법
아다그라드(Adagrad)
- 변수의 업데이트 횟수에 따라 학습률(Learning rate)를 조절하는 옵션이 추가된 최적화 방법
- 변화하지 않은 변수들은 학습률(step size)를 크게하고, 반대로 많이 변화한 변수들에 대해서는 학습률 줄임
- 많이 변화한 변수는 최적값에 근접했을 것이라는 가정에 작은 크기로 이동하면서 세밀한 값을 조정하고, 반대로 적게 변화한 변수들은 학습률을 크게하여 빠르게 loss값을 줄임
알엠에스프롬(RMSProp)
- 아다그라드(Adagrad)는 학습을 계속 진행하면, 나중에 학습률이 지나치게 떨어진다는 단점이 있는데 이부분을 개선함
- 순간기울기(gradient)의 제곱값을 더해나가면서 구한 부분을 합이 아니라 지수평균으로 바꾸어서 대체함
- 최근 변화량의 변수간 상대적인 크기 차이 유지가능
아담(Adam)
- 알엠에스프롬(RMSProp)과 모멘텀(Momentum) 두가지 합친 방법
- 방향과 학습률 두가지를 모두 잡음
- 학습률을 줄여나가고 속도를 계산하여 학습의 갱신도강도를 적응적으로 조정해나가는 방법
- 매개변수 공간을 효율적으로 탐색해주며, 하이퍼파라미터 '편향 보정'이 진행됨
- 가장 많이 사용하는 Optimizer 알고리즘임(Optimizer뭘 써야할지 모르겠다면 Adam)



| 고급 경사 하강법 | 개요 | 효과 | 케라스 사용법 |
| 확률적 경사 하강법(SGD) | 랜덤하게 추출한 일부 데이터를 사용해 더 빨리, 자주 업데이트를 하게 하는 것 | 속도 개선 | keras.optimizers.SGD(lr=0.1) 케라스 최적화 함수 이용 |
| 모멘텀 (Momentum) | 관성의 방향을 고려해 진동과 폭을 줄이는 효과 | 정확도 개선 | keras.optimizers.SGD(lr=0.1, momentum=0.9) 모멘텀 계수를 추가 |
| 네스테로프 모멘텀(NAG) | 모멘텀이 이동시킬 방향으로 미리 이동해서 그레이디언트를 계산, 불필요한 이동을 줄이는 효과 | 정확도 개선 | keras.optimizers.SGD(lr=0.1, momentum=0.9, nesterov=True) 네스테로프 옵션 추가 |
| 아다그라드(Adagrad) | 변수의 업데이트가 잦으면 학습률을 적게하여 이동 보폭을 조절하는 방법 | 보폭 크기 개선 | keras.optimizers.Adagrad(lr=0.01, epsilon=1e-6) 아다그라드 함수 사용 ※epsilon, rho, decay 같은 파라미터는 바꾸지 않고 사용하기를 권장 (lr = learning rate값만 적절히 조절) |
| 알엠에스프롬(RMSProp) | 아다그라드의 보폭 민감도를 보완한 방법 | 보폭 크기 개선 | keras.optimizers.RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0) 알엠에스프롬 함수 사용 |
| 아담(Adam) | 모멘텀과 알엠에스프롬 방법을 합친 방법 | 정확도와 보폭 크기 개선 | keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0) 아담 함수 사용 |
Reference : 딥러닝을 이용한 자연어 처리 입문, 모두의 딥러닝, 모두의 인공지능
'인공지능 관련' 카테고리의 다른 글
| verbose (0) | 2021.06.09 |
|---|---|
| 대표적인 오차 함수 (0) | 2021.06.01 |
| 사이킷런 (scikit-learn) 기초 (0) | 2021.05.21 |
| 인공지능 개발 환경 만들기 (0) | 2021.05.18 |
| 결정 트리 (0) | 2021.05.12 |