재귀 호출(recursive call)

재귀 호출

 

자기 자신을 호출하여 순환 수행

재귀호출방식을 사용하면 프로그램의 크기를 줄이고 간단하게 작성 가능!

 

But, 실무에서 쓰면 욕먹음(되도록 쓰지말자)

1. 시간복잡도 계산이 반복문에 비해 어렵다
2. 반복문보다 메모리 사용량 많고, 수행 시간이 길어 질 수 있음
3. 함수 호출 많이해서 StackOverFlow 가능성있음
4. 종결조건을 확실하게 하지않으면 무한반복
5. 무한 반복이 일어나면 CPU 크래쉬 발생(반복문은 메모리 부족하면 알아서 멈춤)

 

 

재귀 호출 예시1 - 팩토리얼

 

private int factorial(int n){
	if(n == 1) return 1;
    return n * factorial(n - 1);
}

 

 

재귀 호출 예시2 - 피보나치 수열

 

0과 1로  시작하고 이전의 두 수 합을 다음 항으로 하는  수열을 피보나치라고 함

 

private int Fibonacci(int n) 
{ 	
	if (0 == n) return 0;
	if (1 == n) return 1;
	return Fibonacci(n - 1) + Fibonacci(n - 2);
}

 

 

재귀호출 문제점

 

 

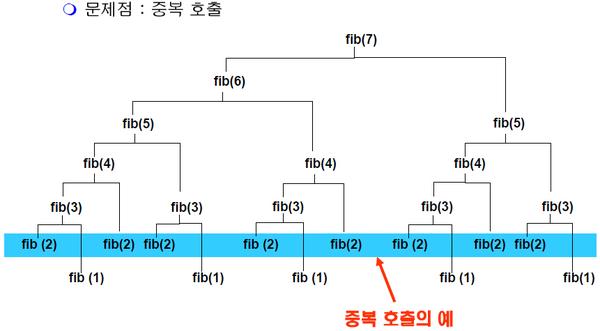
※중복 호출 문제를 해결하기 위해 메모이제이션을 사용

 

메모이제이션(memoization) : 컴퓨터 프로그램을 실행할 때 이전에 계산한 값을 메모리에 저장해서 매번 다시 계산하지 않도록 하여 전체적인 실행속도를 빠르게 하는 기술(동적 계획법의 핵심이 되는 기술)

 

	static long[] arr = new long[51];	

	static long fiboMemoization(int N) {
		if (N == 0) {
			return arr[0];
		} else if (N == 1) {
			return arr[1];
		} else if (arr[N] != 0) {
			return arr[N];
		} else {
			return arr[N] = fiboMemoization(N - 1) + fiboMemoization(N - 2);
		}
	}

 

 

동적 계획 알고리즘 (DP, Dynamic Programming)

• 그리디 알고리즘과 같이 최적화 문제를 해결하는 알고리즘
• 먼저 입력 크기가 작은 부분 문제들을 모두 해결한 후에 그 해들을 이용하여 보다 큰 크기의 부분 문제들을 해결하여, 최종적으로 원래 주어진 입력의 문제를 해결하는 알고리즘

 

 

재귀 피보나치

private static int recurSiveFibo(int i) {
    if (i <= 1) {
        return i;
    } else {
        return recurSiveFibo(i - 2) + recurSiveFibo(i - 1);
    }
}

 

 

 

동적 계획 알고리즘 (DP, Dynamic Programming) 사용한 피보나치

private static int getDpFibo(int fiboCnt) {
   fiboDpArray = new int[fiboCnt + 1];
        
   fiboDpArray[0] = 0;
   fiboDpArray[1] = 1;
        
   if (fiboCnt > 1) {
     for (int i = 2; i <= fiboCnt; i++) {
        fiboDpArray[i] = fiboDpArray[i - 2] + fiboDpArray[i - 1];
     }
   }
        
    return fiboDpArray[fiboCnt];
}

 

• 메모이제이션(memoization)을 재귀적 구조에 사용하는 것보다 반복적 구조로 DP를 구현한 것이 성능 면에서 효율적임
• 재귀적 구조는 내부에 시스템 호출 스택을 사용하는 오버헤드가 발생하기 때문임